回顾和复习常见神经网络结构的底层原理————FNN（卷积神经网络）

Day2：FNN

1. 神经元(neuron)

        神经元是神经网络的基本计算单元，也被称作节点(node)或者单元(unit)。它可以接受来自其他神经元的输入或者是外部的数据，然后计算一个输出。

        每个输入值都有一个权重(weight)，权重的大小取决于这个输入相比于其他输入值的重要性。然后在神经元上执行一个特定的函数 f， 定义如下图所示，这个函数会该神经元的所有输入值以及其权重进行一个操作。

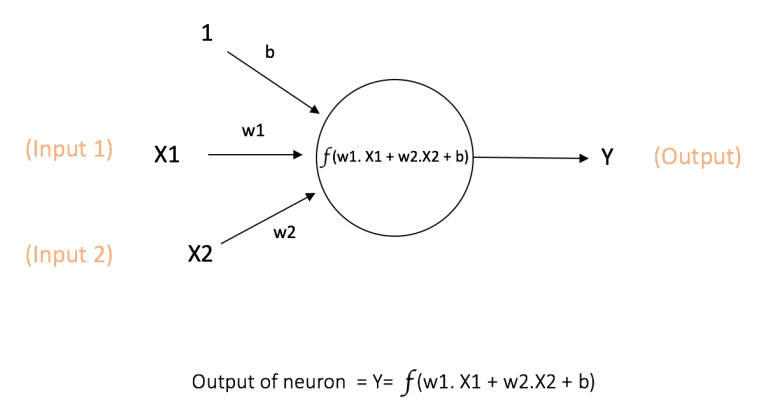
由上图可以看到，除了权重外，还有一个输入值是b的偏置值bias。这里的函数 f 就是一个被称为激活函数的非线性函数。它的目的是给神经元的输出引入非线性。因为在现实世界中的数据都是非线性的，因此我们希望神经元都可以学习到这些非线性的表示。

• 设置偏置值bias的原因

Y = kx + b（直线方程）如果没有bias，这条线将始终穿过原点，并且Y的值只取决于一个参数k，即斜率。可能会得到更差的拟合。

而bias代表偏差，接受任何数字，并具有移动图形的活动，因此能够表示更复杂的情况。

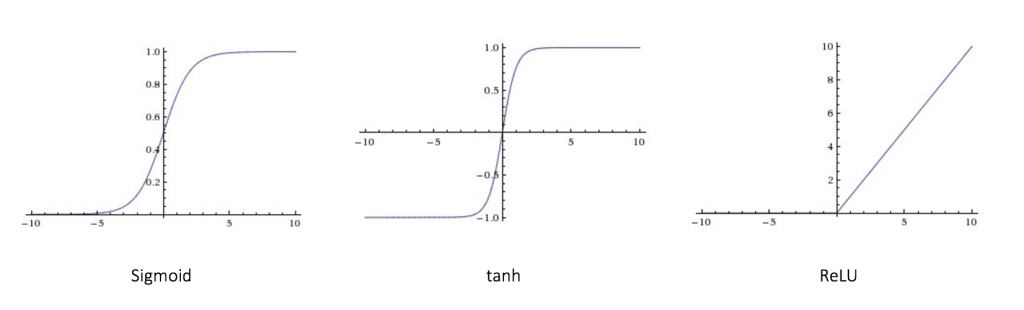
• 常见的激活函数

2. FNN

        前馈神经网络（Feedforward Neural Network， FNN ）第一个也是最简单的一种人工神经网络。其每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层。第0层叫做输入层，最后一层叫做输出层，其他中间层叫做隐藏层。整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示。

• 输入神经元：位于输入层，主要是传递来自外界的信息进入神经网络中，比如图片信息，文本信息等，这些神经元不需要执行任何计算，只是作为传递信息，或者说是数据进入隐藏层。
• 隐藏神经元：位于隐藏层，隐藏层的神经元不与外界有直接的连接，它都是通过前面的输入层和后面的输出层与外界有间接的联系，因此称之为隐藏层，上图只是有1个网络层，但实际上隐藏层的数量是可以有很多的，远多于1个，当然也可以没有，那就是只有输入层和输出层的情况了。隐藏层的神经元会执行计算，将输入层的输入信息通过计算进行转换，然后输出到输出层。
• 输出神经元：位于输出层，输出神经元就是将来自隐藏层的信息输出到外界中，也就是输出最终的结果，如分类结果等。

        假设$l$层共有$M$个节点，$l+1$层共有$N$个节点，$W^l_{nm}$是第$l$层第$m$个节点到第$l+1$层第$n$个节点的权重，$b^{l+1}_n$是第$l+1$层第$n$个节点的偏置，$f^{l+1}_n$是第$l+1$层第$n$个节点的偏置函数，则：

$x^{l+1}n=f^{l+1}_n(\sum{m=1}^{M}{w^{l+1}_{nm}x^l_m}+b^{l+1}_n)$

这样前馈神经网络通过逐层的信息传递，得到网络最后的输出

3. 反向传播

        用神经网络对数据进行建模，就是要找到最合适的参数（权重和偏置）对数据进行最佳逼近。通常会设计一个损失函数来度量逼近效果，最优参数应使得损失函数最小化。神经网络可以视为一个非常复杂的复合函数，求解最优参数时，需要进行链式求导，形成了梯度的反向传播。（数学推导略）

4.梯度消失和梯度爆炸

（1）原理

         训练神经网络，尤其是深度神经网络时，面临的一个问题是梯度消失或者梯度爆炸，也就是神经元上的梯度会变得非常小或者非常大，从而加大训练的难度。

        定义：梯度消失（Vanishing Gradient Problem，或称梯度弥散）的意思是，在误差反向传播的过程中，误差经过每一层传递都会不断衰减，当网络层数很深时，神经元上的梯度也会不断衰减，导致前面的隐含层神经元的学习速度慢于后面隐含层上的神经元。

$\delta^{(l)}=f’_l(x^{(l)})\odot(W^{(l+1)})^T\delta^{(l+1)}$

误差从输出层反向传播时，在每一层都要乘以该层的激活函数的导数，如果导数$f’_l(x^{(l)})$的值域小于1，甚至如Sigmoid函数在两端的饱和区导数趋于0，那么梯度就会不断衰减甚至消失。

        与之相对的问题是梯度爆炸（Exploding Gradient Problem），也就是前面层中神经元的梯度变得非常大。与梯度消失不太一样的是，梯度爆炸通常产生于过大的权重W。

梯度消失通常出现在深层网络和采用了不合适的损失函数（sigmoid）的情形，梯度爆炸一般出现在深层网络和权值初始化值太大的情况下。

• $sigmoid’(x)=sigmoid(x)(1-sigmoid(x))\in[0,0.25]$

（2）解决

• 对于梯度消失问题，可以选择导数比较大的激活函数，比如ReLU激活函数。

        Sigmoid函数和Tanh函数都属于两端饱和型激活函数，使用这两种激活函数的神经网络，在训练过程中梯度通常会消失，因此可以选择其他激活函数来替代：

        ReLU激活函数在正数部分的导数恒为1，每层网络都可以得到相同的更新速度，因此在深层网络中不会产生梯度消失和梯度爆炸的问题。

• 对于梯度爆炸问题，可以采取梯度截断和权重正则化的方法。

        梯度截断这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度截断阈值，然后在更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。

        权重正则化就是在损失函数中，加入对网络的权重进行惩罚的正则化项，比如权重的L1正则化或者L2正则化。如果发生梯度爆炸，权值的范数会变得非常大，通过正则化项进行惩罚，可以限制权重的值，从而减轻梯度爆炸的问题。