hot100 (80 / 100)
Published:
2025-1-24开始刷hot100,计划2025-03-15前刷完。最近一次更新是2025-03-11。暂时到这里截止了 (86 / 100) ,开别的篇章剩下的难题慢慢写了,不一天到晚死磕了。
一眼不会写
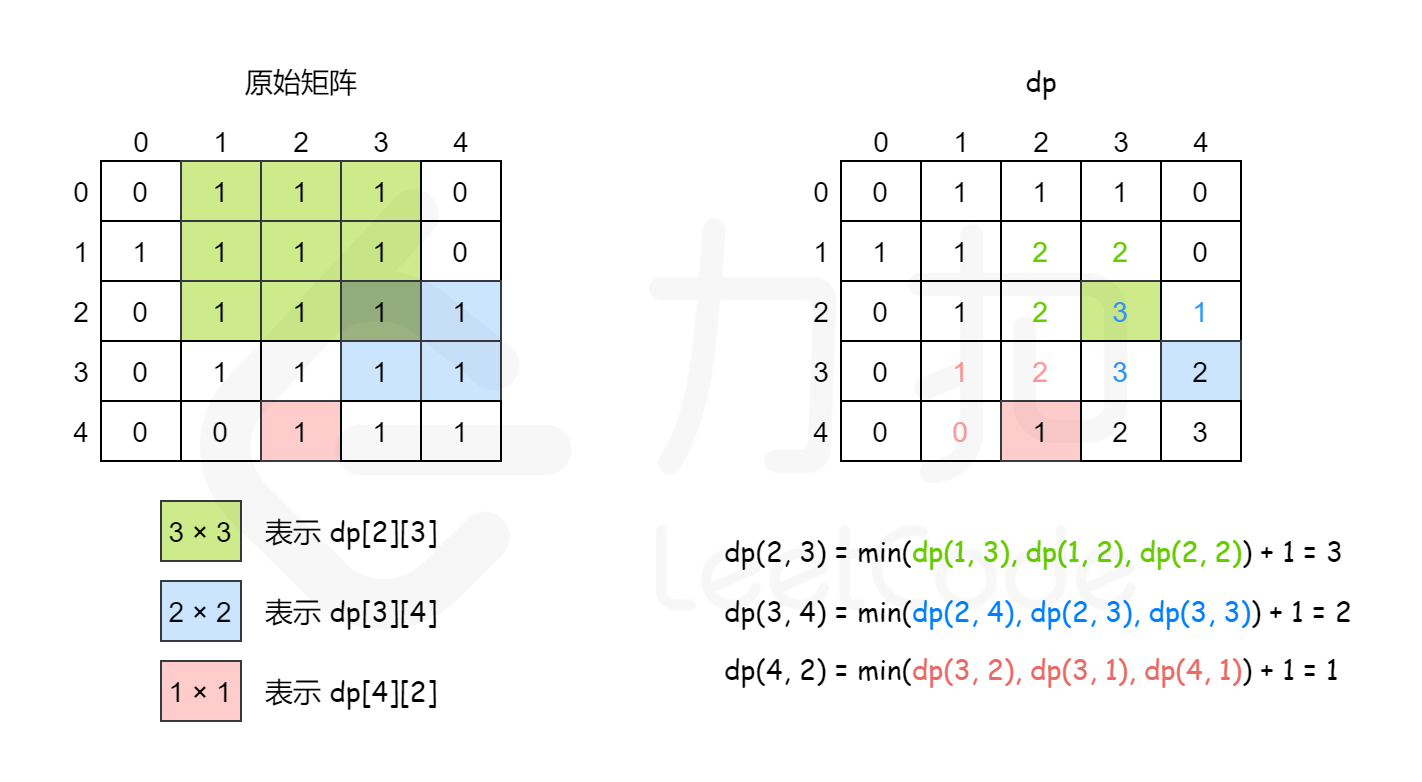
没想到是dp 利用min{dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]}就可以判断最右下角的1能否合一起构成一个大正方形,想到了还是比较easy的。
class Solution {
public:
int dp[300][300];
int maximalSquare(vector<vector<char>>& matrix) {
int ans=0;
for(int i = 0; i < matrix.size(); i++){
for(int j = 0; j < matrix[i].size(); j++){
if(matrix[i][j]=='1'){
if(i==0||j==0) dp[i][j]=1;
else dp[i][j]=min(min(dp[i-1][j],dp[i-1][j-1]),dp[i][j-1]) + 1;
}
ans = max(ans,dp[i][j]);
}
}
return ans * ans;
}
};
方法:哈希表+双向列表
(1)一旦出现键+值,就要想到哈希表
(2)在双向链表的实现中,使用一个伪头部(dummy head)和伪尾部(dummy tail)标记界限,这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。
struct node{
int key, val;
node *pre, *next;
node() : key(-1), val(-1), pre(NULL), next(NULL){}
node(int a, int b) : key(a), val(b), pre(NULL), next(NULL){}
};
class LRUCache {
protected:
unordered_map<int, node*> mp;
node *head, *tail;
int size, capacity;
public:
LRUCache(int a) {
size = 0, capacity = a;
head = new node(), tail = new node();
head -> next = tail;
tail -> pre = head;
}
int get(int key) {
if(mp.count(key)){
node *n = mp[key];
n -> next -> pre = n -> pre;
n -> pre -> next = n -> next;
n -> next = head -> next;
n -> next -> pre = n;
head -> next = n;
n -> pre = head;
return n -> val;
}
return -1;
}
void put(int key, int value) {
if(mp.count(key)){
node* n = mp[key];
n -> val = value;
n -> pre -> next = n -> next;
n -> next -> pre = n -> pre;
n -> next = head -> next;
head -> next -> pre = n;
n -> pre = head;
head -> next = n;
}
else{
node* n = new node(key, value);
mp[key] = n;
n -> next = head -> next;
n -> pre = head;
head -> next -> pre = n;
head -> next = n;
size++;
if(size > capacity){
node *DeleteNode = tail -> pre;
tail -> pre -> pre -> next = tail;
tail -> pre = tail -> pre -> pre;
mp.erase(DeleteNode -> key);
delete DeleteNode;
size--;
}
}
}
};
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache* obj = new LRUCache(capacity);
* int param_1 = obj->get(key);
* obj->put(key,value);
*/
要细心一点,注意插入双向指针的操作;注意删除哈希表的键和节点空间,防止内存泄漏和冗余。
当时一下子不知道咋dp处理这个正数和负数。所有数组的和是sum,所有设为负数的数组元素和是neg,则题目要求是否存在(sum - neg) - neg = taget。转换式子得neg = (sum - taget) / 2,此时就可以用简单的01背包算。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for(auto num : nums) sum += num;
if((sum - target) % 2 || sum < target) return 0;
int len = (sum - target) / 2;
vector<int> dp(len + 1);
dp[0] = 1;
for(auto num : nums){
for(int i = len; i - num >= 0; i--){
if(dp[i - num] > 0) dp[i] = dp[i - num] + dp[i];
}
}
return dp[len];
}
};
有点后悔提前放弃,脑袋里只想着在创一个结构体。其实这道题本身不难。
class Trie {
private:
vector<Trie*> v;
bool isEnd;
Trie* searchPrefix(string prefix){
Trie* node = this;
for(char ch : prefix){
ch -= 'a';
if(node -> v[ch] == nullptr) return nullptr;
node = node -> v[ch];
}
return node;
}
public:
Trie() {
v = vector<Trie*>(26);
isEnd = 0;
}
void insert(string word) {
Trie *node = this;
for(char ch : word){
ch -= 'a';
if(node -> v[ch] == nullptr) node -> v[ch] = new Trie();
node = node -> v[ch];
}
node -> isEnd = 1;
}
bool search(string word) {
Trie* node = this -> searchPrefix(word);
return node != nullptr && node -> isEnd;
}
bool startsWith(string prefix) {
return this->searchPrefix(prefix) != nullptr;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/
旋转后只保证了数组的局部是有序的,但可以发现的是,我们将数组从中间分开成左右两部分的时候,一定有一部分的数组是有序的,并根据有序的那个部分确定我们该如何改变二分查找的上下界
class Solution {
public:
int find(int l, int r, vector<int>& nums, int target){
int mid;
while(l < r){
mid = (l + r + 1) / 2;
if(nums[mid] > target) r = mid - 1;
else l = mid;
}
if(nums[l] == target) return l;
else return -1;
}
int check(int l, int r, vector<int>& nums, int target){
if(l == r) return nums[l] == target ? l : -1;
int mid = (l + r) / 2, ans = -1;
if(nums[mid] > nums[l]){
int a = find(l, mid, nums, target);
if(a == -1) ans = check(mid + 1, r ,nums, target);
else ans = a;
}
else{
int a = find(mid + 1, r ,nums, target);
if(a == -1) ans = check(l, mid, nums, target);
else ans = a;
}
return ans;
}
int search(vector<int>& nums, int target) {
int n = nums.size();
if(n == 0) return -1;
return check(0, n - 1, nums, target);
}
};
其实是一个先猜想后证实的双指针问题。
假设height[r]的值大于height[l],那么area = height[l] * (r - l),此时,如果移动r会出现以下两种情况:
height[r'] >= height[r],此时area‘ = min(height[r'], height[h]) * (r - l - k) = height[h] * (r - l - k),即比area小height[r'] < height[r],此时min(height[r'], height[h]) <= height[h],即area' <= area
所以不能移动较大的指针,只能探索较小的指针的可能性,因此直接利用双指针两头遍历一边即可。
class Solution {
public:
int maxArea(vector<int>& height) {
int l = 0, r = height.size() - 1, ans = 0;
while(l < r){
ans = max(min(height[l], height[r]) * (r - l), ans);
height[l] > height[r] ? r-- : l++;
}
return ans;
}
};
用dp写要考虑的东西太麻烦了。终于来学马拉车了,之前懒惰推了好久,这道题真是死活过不去。
(1)朴素方法:
abac e caba对每一个i,向两边扩展直接匹配。考虑到奇偶性的问题,我们插入#,把整个字符串变成奇。此时复杂度为O(N)。
class Solution {
public:
string longestPalindrome(string ss) {
string s = "#", ans;
for(char ch : ss) s = s + ch + "#";
int n = s.size(), ma = 0, flag = -1;
vector<int> v(n);
for(int i = 0; i < n; i++){
while(s[i - v[i]] == s[i + v[i]]) {
v[i]++;
if(i - v[i] < 0 || i + v[i] >= n) break;
}
if(ma < v[i]){
ma = v[i];
flag = i;
}
}
for(int i = flag - ma + 1; i < flag + ma - 1; i++)
if(s[i] != '#') ans += s[i];
return ans;
}
};
(2)马拉车:
充分利用回文串对称的特性。回文串的臂长里面有回文串的话,另一边也有。用一个数组记录臂长,再往后推。如果臂长里只有一半回文串的话,推的时候改为最小值。这样子就大大减小了两边扩展的时间。
比如说:
#c#b#a#b#c# d#c#b#a#
121216
此时center是下标5的a,right达到了5 + 6 - 1 = 10。当i = 6时,和下标为5 * 2 - 6 = 4的值相同也是1。这样子我们再扩展的话会省掉下大量时间。
以此类推,我们可以得到: #c#b#a#b#c# d#c#b#a#
12121612121
到下一个d时,以此类推得到8,right达到了11 + 8 - 1 = 18。当i = 12时,和下标11 * 2 - 12 = 10的值相同也是1。
但是倒数第二个a要算min(right - i + 1, v[2 * center - i]),因为不能确定之后的。
通过这样的方式,提前缩小了扩展的范围。实现了在朴素方法上的进一步优化。
class Solution {
public:
string longestPalindrome(string ss) {
string s = "#", ans;
for(char ch : ss) s = s + ch + "#";
int center = -1, right = -1, n = s.size();
int ma = -1, flag = -1;
vector<int> v(n);
for(int i = 0; i < n; i++){
if(i <= right) {
v[i] = min(right - i + 1, v[center * 2 - i]);
}
while(s[i - v[i]] == s[i + v[i]]){
v[i]++;
if(i - v[i] < 0 || v[i] + i >= n) break;
}
if(ma < v[i]) ma = v[i], flag = i;
if(i + v[i] > right) right = i + v[i] - 1, center = i;
}
for(int i = flag - ma + 1; i <= flag + ma - 1; i++)
if(s[i] != '#') ans += s[i];
return ans;
}
};
数学找规律题。

class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
for(int i = 0; i < n / 2; i++){
for(int j = 0; j < n; j++){
swap(matrix[i][j], matrix[n - i - 1][j]);
}
}
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++){
swap(matrix[i][j], matrix[j][i]);
}
}
}
};
这道题目的关键在于“刚好”,说明只有一种确切的排序。
我们可以从矮到高的顺序去看,如果已经排好了前i-1矮的位置:
对于第
i高的这个人,排在哪里前面都没有比他高的。只有之后的人站在他的前面才有影响。对于前
i-1个人,如果被排在第i个人后面,他们的影响都+1。
那么我们的排法就是对于第i个人,前面要有$k_i$个空位置给后面的人比他高的人影响。这样的话,之前的人等预先空的位置被后来高的人填满,从而满足这个整好的条件。为了满足这样的排列顺序,我们自定义sort函数:[](const vector& v1, const vector& v2){ return v1[0] < v2[0] || (v1[0] == v2[0] && v1[1] > v2[1]);}从低到高排身高的同时,对于相同身高约难满足的越先排(因为相同身高也算影响,从而实现后面的人影响前面的人,之前放下去同身高的也影响不到现在排的这个。)
class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort(people.begin(), people.end(), [](const vector<int>& v1, const vector<int>& v2){
return v1[0] < v2[0] || (v1[0] == v2[0] && v1[1] > v2[1]);
});
int n = people.size();
vector<vector<int>> ans(n);
for(int i = 0; i < n; i++){
int place = people[i][1] + 1;
for(int j = 0; j < n; j++){
if(ans[j].empty()){
place--;
if(place == 0){
vector<int> temp{people[i][0], people[i][1]};
ans[j] = temp;
break;
}
}
}
}
return ans;
}
};
这道题的核心就在于,前面的人对自己没影响,后面的人对自己有影响。因此只用考虑后面的人,给后面的人留位置就行了。
非一遍过
内存超限,给每一个节点的父节点都用栈存起来了。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
void check(TreeNode* node, map<TreeNode*, stack<TreeNode*>> &mp){
if(node->left!=nullptr){
mp[node->left] = mp[node];
mp[node->left].push(node->left);
check(node->left, mp);
}
if(node->right!=nullptr){
mp[node->right] = mp[node];
mp[node->right].push(node->right);
check(node->right, mp);
}
return;
}
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
TreeNode* r = root;
map<TreeNode*, stack<TreeNode*>> mp;
check(root, mp);
unordered_set<TreeNode*> s;
while(!mp[p].empty()) {
s.insert(mp[p].top());
mp[p].pop();
}
while(!mp[q].empty()){
if(s.count(mp[q].top())) return mp[q].top();
mp[q].pop();
}
return root;
}
};
稍微修改了一点,看到题目中的键值各不相同,所以只存父节点指针。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
map<int, TreeNode*> mp;
void check(TreeNode* node){
if(node->left!=nullptr){
mp[node->left->val] = node;
check(node->left);
}
if(node->right!=nullptr){
mp[node->right->val] = node;
check(node->right);
}
return;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
TreeNode* r = root;
check(root);
unordered_set<TreeNode*> s;
TreeNode *i = p, *j = q;
while(i!=nullptr) {
s.insert(i);
i = mp[i->val];
}
while(j!=nullptr){
if(s.count(j)) return j;
j = mp[j->val];
}
return root;
}
};
没有想到非暴力做法,使用单调栈
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n = temperatures.size();
vector<int> ans(n);
stack<int> s;
for(int i = 0; i < n; i++){
while(!s.empty() && temperatures[i] > temperatures[s.top()]){
ans[s.top()] = i - s.top();
s.pop();
}
s.push(i);
}
return ans;
}
};
这道题的本质是判断是否有环,但写成了是否通路
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<bool> a(numCourses, 1), b(numCourses);
map<int, vector<int>> tree;
for(int i = 0; i < prerequisites.size(); i++){
tree[prerequisites[i][1]].emplace_back(prerequisites[i][0]);
a[prerequisites[i][0]] = 0;
}
for(int i = 0; i < numCourses; i++){
if(a[i]){
queue<int> q;
q.push(i);
while(!q.empty()){
int top = q.front();
b[top] = 1;
for(auto j : tree[top])
q.push(j);
q.pop();
}
}
}
for(int i = 0; i < numCourses; i++){
if(!b[i]) return 0;
}
return 1;
}
};
没有考虑到小根堆和栈的stl的pop弹出是不一样的
class MinStack {
stack<int> s;
priority_queue<int> p;
public:
MinStack() {
}
void push(int val) {
p.push(val);
s.push(val);
}
void pop() {
p.pop();
s.pop();
}
int top() {
return s.top();
}
int getMin() {
return p.top();
}
};
需要一个辅助栈记录每一个元素进入时,当前栈内的最小值。
class MinStack {
stack<int> s1, s2;
public:
MinStack() {
s2.push(INT_MAX);
}
void push(int val) {
s1.push(val);
s2.push(min(val, s2.top()));
}
void pop() {
s1.pop(), s2.pop();
}
int top() {
return s1.top();
}
int getMin() {
return s2.top();
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(val);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->getMin();
*/
回文串判断错了,不是只用判断前一半等于后一半,且复杂度过高substr导致O(N^3)的时间复杂度
class Solution {
public:
int countSubstrings(string s) {
int len = s.size(), sum = 0;
for(int i = 0; i < len; i++){
for(int j = 0; j <= i; j++){
int num = i - j + 1;
int mid = num / 2;
if(num % 2 == 1){
if(s.substr(j, mid) == s.substr(j + mid + 1, mid)) sum++;
}
else{
if(s.substr(j, mid) == s.substr(j + mid, mid)) sum++;
}
}
}
return sum;
}
};
其实很简单啊这道题,就是一个双指针。分别枚举一下奇数回文子串和偶数回文子串。
class Solution {
public:
int countSubstrings(string s) {
int len = s.size(), l, r, sum = 0;
for(int i = 0; i < len; i++){
sum++;
l = i - 1, r = i + 1;
while(l >= 0 && r < len){
if(s[l] == s[r]) sum++;
else break;
l--, r++;
}
l = i, r = i + 1;
while(l >= 0 && r < len){
if(s[l] == s[r]) sum++;
else break;
l--, r++;
}
}
return sum;
}
};
这个写法超时了。
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
vector<int> ans;
unordered_set<string> unset;
do {
unset.insert(p);
} while (next_permutation(p.begin(), p.end()));
for(int i = 0; i + p.size() <= s.size(); i++){
string ss = s.substr(i, p.size());
if(unset.count(ss)) ans.emplace_back(i);
}
return ans;
}
};
用滑动窗口优化,记录组成的字母个数就行了。要思考到字母异位词是通过重新排列不同单词或短语的字母而形成的单词或短语,并使用所有原字母一次。的本质是字符数量相同就行了。
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
vector<int> ans, ss(26), pp(26);
if(s.size() < p.size()) return ans;
for(int i = 0; i < p.size(); i++) ss[s[i] - 'a']++, pp[p[i] - 'a']++;
if(ss == pp) ans.emplace_back(0);
for(int i = 1; i + p.size() <= s.size(); i++){
ss[s[i - 1] -'a']--, ss[s[i + p.size() - 1] - 'a']++;
if(ss == pp) ans.emplace_back(i);
}
return ans;
}
};
很费劲的一道题啊,注意的细节很多。用栈存储[和],还要判断[前面化成字符串的数字。自己做了很久但终于debug对了。
class Solution {
public:
string decodeString(string s) {
stack<int> st;
string ans, be, re, af;
for(int i = 0; ; i++){
if(i >= s.size()) break;
if(s[i] >= '0' && s[i] <= '9') continue;
if(s[i] == '[') st.push(i);
else if(s[i] == ']') {
int pre = st.top();
//cout << pre << endl;
st.pop();
string num;
for(int j = 1; j <= pre; j++){
if(s[pre - j] >= '0' && s[pre - j] <= '9') num = s[pre - j] + num;
else break;
}
int len = num.size(), n = 0;
for(int j = 0; j < len; j++){
int temp = num[j] - '0';
n = n * 10 + temp;
}
be = s.substr(0, pre - len);
re = s.substr(pre + 1, i - pre - 1);
af = s.substr(i + 1, s.size() - i);
//cout << be << ' ' << af << endl;
ans = be;
for(int j = 1; j <= n; j++){
ans += re;
}
i = ans.size() - 1;
ans += af;
s = ans;
//cout << s << endl;
}
}
return s;
}
};
写了半天的DFS,但用一个全局的vis布尔数组无法准确判断环,重新看了一下DFS拓扑排序的题解视频。
class Solution {
public:
map<int, vector<int>> tree;
vector<int> vis, a;
void check(int node){
if(vis[node] > a[node]) return;
vis[node] += 1;
for(auto i:tree[node]){
check(i);
}
return;
}
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
a = vector<int>(numCourses + 1);
vis = vector<int>(numCourses + 1);
for(int i = 0; i < prerequisites.size(); i++){
tree[prerequisites[i][1]].emplace_back(prerequisites[i][0]);
a[prerequisites[i][0]]++;
}
for(int i = 0; i < numCourses; i++){
if(a[i] == 0){
tree[numCourses].emplace_back(i);
a[i] = 1;
// printf("%d", i);
}
}
check(numCourses);
for(int i = 0; i < numCourses; i++)
if(vis[i] != a[i]) return 0;
return 1;
}
};
我们选择dfs,每次选择出度为0的节点入栈(摘出去。对于任意一个节点,它在搜索的过程中有三种状态,即:
「未搜索」:我们还没有搜索到这个节点(状态默认为0);
「搜索中」:我们搜索过这个节点,但还没有回溯到该节点,即该节点还没有入栈,还有相邻的节点没有搜索完成)(状态设置为1。在一次dfs中再次经过正在搜索状态的节点,说明**有环**。);
「已完成」:我们搜索过并且回溯过这个节点,即该节点已经入栈(出度为1,摘出去),并且所有该节点的相邻节点都出现在栈的更底部的位置,满足拓扑排序的要求(状态设置为2,已经被摘出去了,可以忽略对他的搜索)。
class Solution {
public:
vector<vector<int>> v;
vector<int> vis;
void dfs(int n){
vis[n] = 1;
for(auto i : v[n]){
if(vis[i] == 1) return;
else if(vis[i] == 2) continue;
else dfs(i);
}
vis[n] = 2;
}
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
v = vector<vector<int>>(numCourses);
vis = vector<int>(numCourses);
for(auto p : prerequisites) v[p[1]].emplace_back(p[0]);
for(int i = 0; i < numCourses; i++) {
if(!vis[i]) dfs(i);
}
for(auto i : vis){
if(i != 2) return false;
}
return true;
}
};
二分条件又给记忘了。其实还是比较简单的,重点巩固了一下mid何时向上取整和向下取整。核心是要求每次变换的时候,在保证`l`只能变大,`r`只能变小的前提下,`l`和`r`的值至少要变一个。而/2是向下取整,所以说r = mid - 1时, 极端情况下mid的计算可能等于l,但如果又满足l = mid的条件时,l,r都不会改变,造成死循环,因此在r = mid - 1的条件下选择向上取整。
class Solution {
public:
int n;
int FindFirst(vector<int>& nums, int target){
int l = 0, r = n - 1, mid;
while(l < r){
mid = (l + r) / 2;
if(nums[mid] < target) l = mid + 1;
else r = mid;
}
if(nums[l] == target) return l;
return -1;
}
int FindSecond(vector<int>& nums, int target){
int l = 0, r = n - 1, mid;
while(l < r){
mid = (l + r + 1) / 2;
if(nums[mid] <= target) l = mid;
else r = mid - 1;
}
if(nums[l] == target) return l;
return -1;
}
vector<int> searchRange(vector<int>& nums, int target) {
n = nums.size();
vector<int> ans;
if(n > 0) ans.emplace_back(FindFirst(nums, target)), ans.emplace_back(FindSecond(nums, target));
else ans.emplace_back(-1), ans.emplace_back(-1);
return ans;
}
};
有纠结了一下二分,补充了一点二分的心得。然后答案输出是原下标,改的时候没注意,老写错。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> ans;
vector<pair<int,int>> v;
for(int i = 0; i < nums.size(); i++) v.emplace_back(make_pair(nums[i], i));
sort(v.begin(), v.end());
for(int i = 0; i < nums.size(); i++){
int l = 0, r = nums.size() - 1, num = v[i].first;
while(l < r){
int mid = (l + r + 1) / 2;
if(v[mid].first + num > target) r = mid - 1;
else l = mid;
}
// cout<<nums[l] <<"+"<< nums[i]<<endl;
// cout<<l<<" "<<i<<endl;
if(v[l].first + v[i].first == target && v[l].second != v[i].second){
ans.emplace_back(v[i].second), ans.emplace_back(v[l].second);
break;
}
}
return ans;
}
};
题目是一个简单的回溯搜索,但是还有很多小细节没有注意到位。比如对长度为1的字符串的考虑,还有在dfs中最后vis[x][y] = 0的还原。
class Solution {
public:
vector<vector<bool>> vis;
vector<vector<char>> v;
vector<int> nx{-1, 1, 0, 0}, ny{0, 0, -1, 1};
int n, m;
string s;
bool flag = 0;
void dfs(int a, int b, int index){
vis[a][b] = true;
if(index == s.size() - 1 && v[a][b] == s[index])
flag = true;
for(int i = 0; i < 4; i++){
int x = a + nx[i], y = b + ny[i];
if(x < 0 || x >= n || y < 0 || y >= m) continue;
else if(vis[x][y]) continue;
else if(v[x][y] == s[index + 1]) {
dfs(x, y, index + 1);
}
}
vis[a][b] = false;
}
bool exist(vector<vector<char>>& board, string word) {
n = board.size(), m = board[0].size();
v = board, s = word;
vis = vector<vector<bool>>(n, vector<bool>(m));
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(v[i][j] == s[0]) dfs(i, j, 0);
if(flag) return 1;
}
}
return 0;
}
};
本来想用set存下表,但是引用啥的不太会区分。看了题解,原来可以用二进制直接枚举。用000, 001, 010 ···来表示状态。
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
int n = nums.size();
vector<vector<int>> ans;
for(int i = 0; i < (1 << n); i++){
vector<int> temp;
for(int j = 0; j < n; j++){
if(i >> j & 1) temp.emplace_back(nums[j]);
}
ans.emplace_back(temp);
}
return ans;
}
};
这样子的组合方式是先把少的用完了,但显然应该把多的先利用进去。
class Solution {
public:
int leastInterval(vector<char>& tasks, int n) {
int num = 0, ans = 0, count = 1;
vector<int> vv(26), v;
for(int i = 0; i < tasks.size(); i++) vv[tasks[i] - 'A']++;
for(int i = 0; i < 26; i++)
if(vv[i] > 0) v.emplace_back(vv[i]), num++;
sort(v.begin(), v.end());
for(int i = num - 1; i - 1 >= 0; i--){
if(v[i] == v[i - 1]) count++;
else break;
}
for(int i = 0; i < num; i++){
int temp = v[i];
for(int j = 0; j < min(num - i, n + 1); j++){
v[i + j] -= temp;
}
ans += (n + 1) * temp;
}
ans -= (n + 1 - count);
return ans;
}
};
应该是先用多的,直接逆序算矩形(因为每次每种都尽可能的用),最后一行多出来余数再加一起(最后做完了,不用等待)。
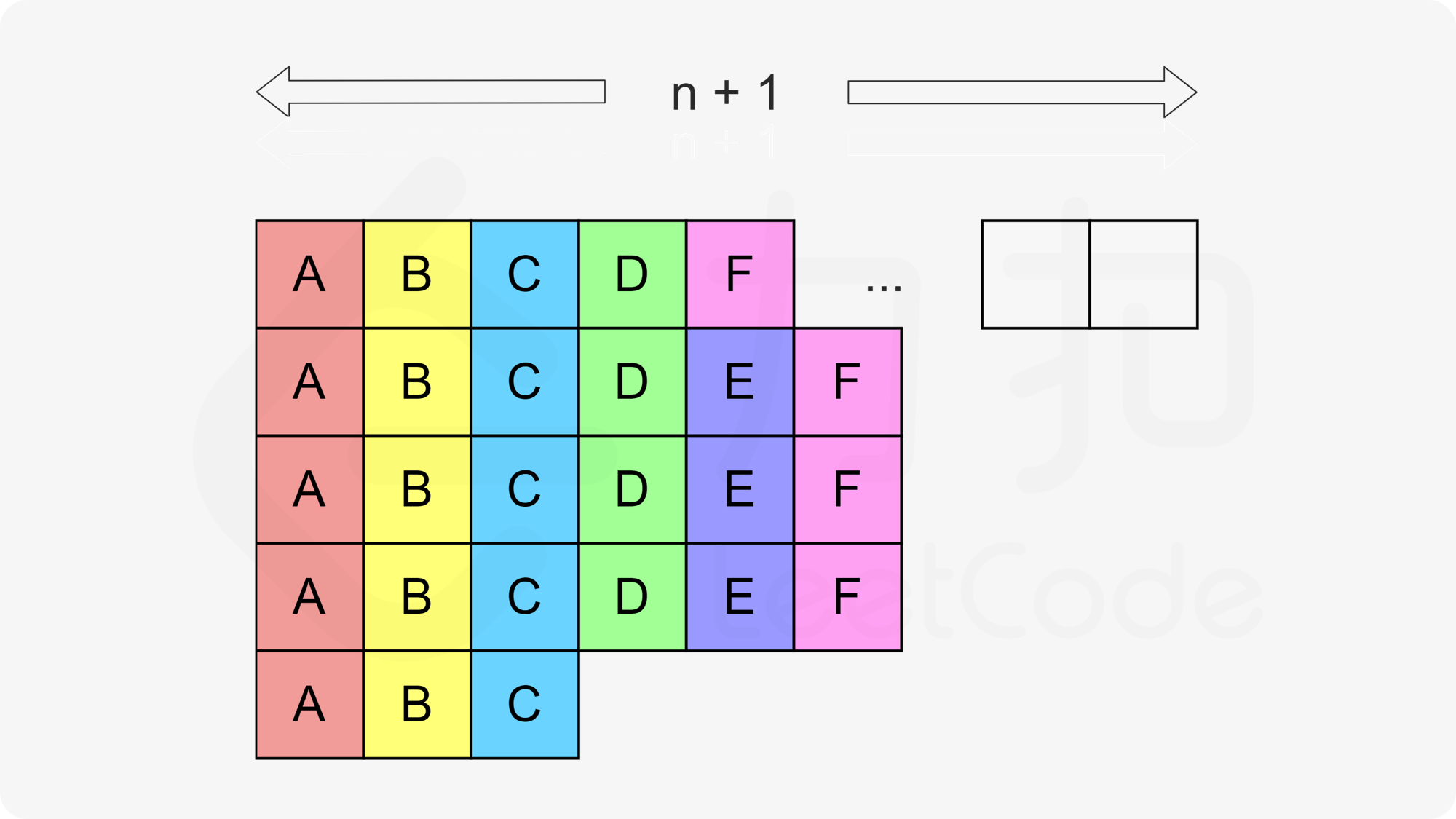
但最后为啥要和tasks.size()作比较——是因为当种类数大于n + 1时,就会不用等待,直接就是总任务数量tasks.size()。(此时再利用ans = (v[0] - 1) * (n + 1)时,n + 1算小了)
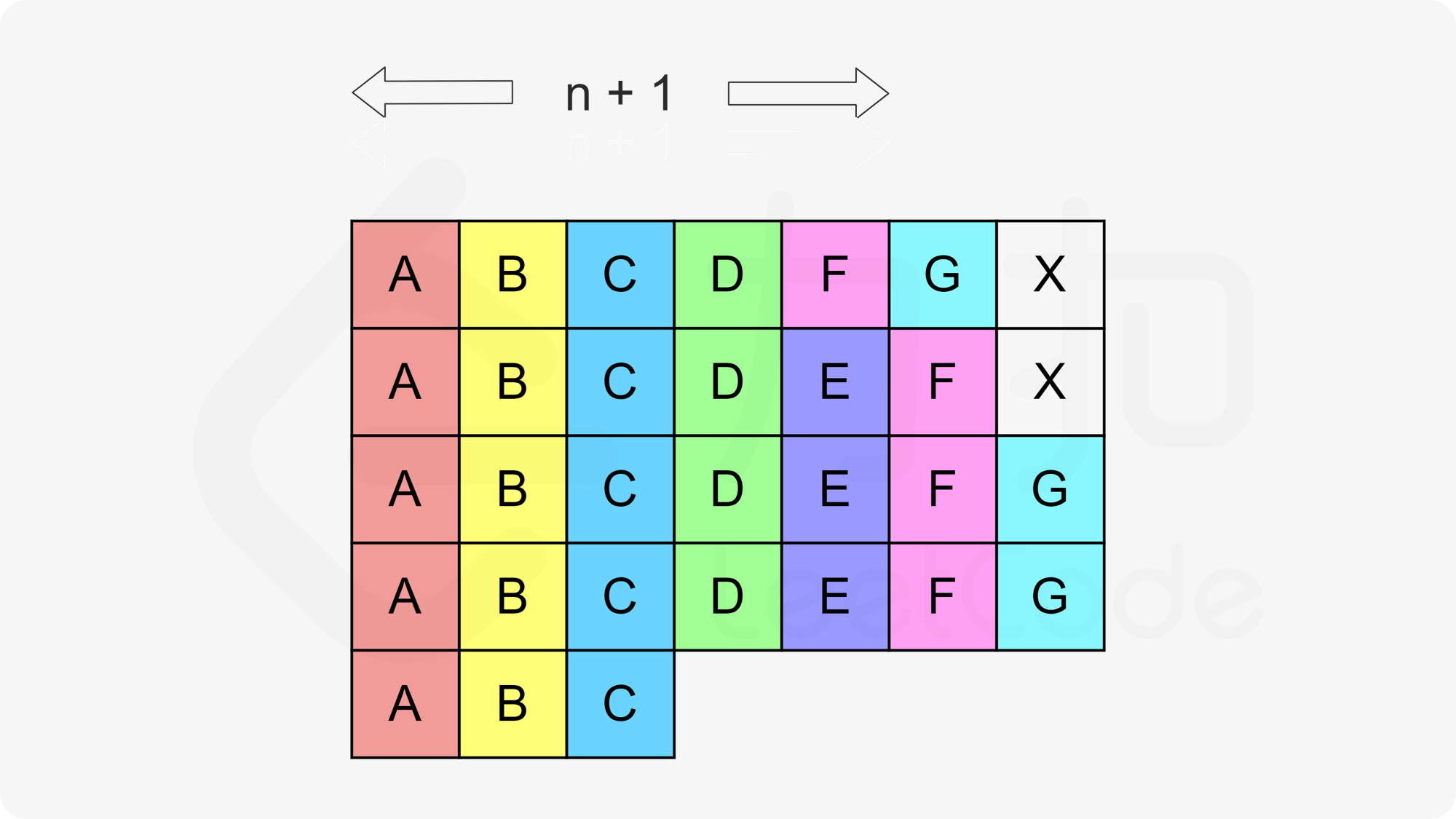
因此最后直接max取最大值就行了,因为最少花费时间不可能比任务时间少,因为直接可以不用单独讨论上面的情况。
class Solution {
public:
int leastInterval(vector<char>& tasks, int n) {
int ans = 0, count = 1;
vector<int> v(26);
for(int i = 0; i < tasks.size(); i++) v[tasks[i] - 'A']++;
sort(v.begin(), v.end(), greater<int>());
ans = (v[0] - 1) * (n + 1);
for(int i = 0; i + 1 < v.size(); i++){
if(v[i] == v[i + 1]) count++;
else break;
}
ans += count;
return max(ans, (int)tasks.size());
}
};
最开始只是考虑一层一层偷,但每一个支路是不一样的。不同支路间,除了分支节点,其他不相互影响。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int dp(vector<int> &v){
int n = v.size(), ans = 0;
vector<int> d = v;
for(int i = 0; i < n; i++){
for(int j = 0; j < i - 1; j++){
d[i] = max(d[j] + v[i], d[i]);
}
ans = max(d[i], ans);
}
return ans;
}
int rob(TreeNode* root) {
vector<int> v;
int flag = 0, sum = 0;
queue<pair<TreeNode*, int>> q;
q.push({root, 1});
while(!q.empty()){
auto [node, depth] = q.front();
if(depth != flag){
if(sum > 0) v.emplace_back(sum);
sum = 0;
flag = depth;
}
sum += node -> val;
if(node -> left != nullptr) q.push({node -> left, depth + 1});
if(node -> right != nullptr) q.push({node -> right, depth + 1});
q.pop();
}
v.emplace_back(sum);
return dp(v);
}
};
直接用两个map,倒着偷(顺着投确实不实现啊)。如果当前节点要偷,那么就分别加上两个子节点没偷时的最大值;如果当前节点不偷,其子节点投或者不偷都不影响其父节点的状态改变,直接加上最大状态的值。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<TreeNode*, int> f, g;
void dfs(TreeNode* root){
if(root == nullptr) return;
dfs(root -> left);
dfs(root -> right);
f[root] = root -> val + g[root -> left] + g[root -> right];
g[root] = max(f[root -> left], g[root -> left]) + max(f[root -> right], g[root -> right]);
}
int rob(TreeNode* root) {
dfs(root);
return max(f[root], g[root]);
}
};
其实这道题目的本质就是给n个点,看能组成多少二叉树。我最开始的思路就是直接递归,左边加一个左子树,右边加一个右子树,两边同时加两个子树。
class Solution {
public:
int ans = 0;
void dfs(int num){
if(num <= 0) {
if(num == 0) ans++;
return;
}
dfs(num - 1);
dfs(num - 1);
dfs(num - 2);
}
int numTrees(int n) {
dfs(n - 1);
return ans;
}
};
但我忽略了在dfs(num - 1) / dfs(num - 2)状态之后的操作是在哪个节点的左边还是右边。因此,不能用这种简单的简单的递归思路。
我们可以采用以序列的任意一个节点做根节点,对两边子树的可能性利用dp记录,排列组合相乘。例如:
xxxx x xxx 就可以用状态转移,左边4个节点的情况乘以右边3个节点的情况。
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = dp[1] = 1;
for(int i = 2; i <= n; i++)
for(int j = 1; j <= i; j++)
dp[i] += dp[j - 1] * dp[i - j];
return dp[n];
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* dfs(TreeNode* node1, TreeNode* node2){
if(node1 == nullptr) return node2;
if(node2 == nullptr) return node1;
TreeNode* node = new TreeNode(node1 ->val + node2 -> val);
node -> left = dfs(node1 -> left, node2 -> left);
node -> right = dfs(node1 -> right, node2 -> right);
return node;
}
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
return dfs(root1, root2);
}
};
这道题的数据范围是3000,因此我是用$n^2logn$过的,并且采用了一些剪枝的做法。
最开始题目读错了,以为是所有的不同下标都要记录一边,所以采用的是两个二分,把排完序从左到右的目标数下表都遍历一遍。
class Solution {
public:
int len;
int FindLeft(int target, vector<int>& nums){
int l = 0, r = len - 1, mid;
while(l < r){
mid = (l + r) / 2;
if(nums[mid] < target) l = mid + 1;
else r = mid;
}
if(nums[l] == target) return l;
return len + 1;
}
int FindRight(int target, vector<int>& nums){
int l = 0, r = len - 1, mid;
while(l < r){
mid = (l + r + 1) / 2;
if(nums[mid] > target) r = mid - 1;
else l = mid;
}
if(nums[l] == target) return l;
return -1;
}
vector<vector<int>> threeSum(vector<int>& nums) {
len = nums.size();
sort(nums.begin(), nums.end());
set<vector<int>> s;
vector<vector<int>> ans;
for(int i = 0; i < len; i++){
for(int j = i + 1; j < len; j++){
int num = 0 - nums[i] - nums[j];
int r = FindRight(num, nums), l = FindLeft(num, nums);
for(int k = l; k <= r; k++){
if(i == k || j == k) continue;
vector<int> temp{nums[i], nums[j], nums[k]};
sort(temp.begin(), temp.end());
s.insert(temp);
// break;
}
}
}
for(vector<int> v : s){
ans.emplace_back(v);
}
return ans;
}
};
结果发现不是,是只用记录可行的组合就行,不用重复记录相同的数值。所以在上面这个做法中,在遇见很多个0的情况下超时了。
因此我发现,一个相同的数字再多,最多也不会在一个组合里超过三个[0, 0, 0]。所以我首先处理一下数据,把相同的数据就最多保留三个。
class Solution {
public:
int len;
int FindLeft(int target, vector<int>& nums){
int l = 0, r = len - 1, mid;
while(l < r){
mid = (l + r) / 2;
if(nums[mid] < target) l = mid + 1;
else r = mid;
}
if(nums[l] == target) return l;
return len + 1;
}
int FindRight(int target, vector<int>& nums){
int l = 0, r = len - 1, mid;
while(l < r){
mid = (l + r + 1) / 2;
if(nums[mid] > target) r = mid - 1;
else l = mid;
}
if(nums[l] == target) return l;
return -1;
}
vector<int> init(vector<int>& nums){
set<int> s;
unordered_map<int, int> mp;
vector<int> res;
for(auto num : nums){
mp[num]++;
s.insert(num);
}
for(auto num : s){
for(int i = 0; i < min(3, mp[num]); i++){
res.emplace_back(num);
}
}
return res;
}
vector<vector<int>> threeSum(vector<int>& v) {
vector<int> nums = init(v);
len = nums.size();
set<vector<int>> s;
vector<vector<int>> ans;
for(int i = 0; i < len; i++){
for(int j = i + 1; j < len; j++){
int num = 0 - nums[i] - nums[j];
int r = FindRight(num, nums), l = FindLeft(num, nums);
for(int k = l; k <= r; k++){
if(i == k || j == k) continue;
vector<int> temp{nums[i], nums[j], nums[k]};
sort(temp.begin(), temp.end());
s.insert(temp);
break;
}
}
}
for(vector<int> v : s){
ans.emplace_back(v);
}
return ans;
}
};
遇到字符串匹配字符数量的,利用滑动窗口。
小插曲,我最开始都是每次不断使用substr这个函数更新ans,因此这样就导致了爆内存。其实直接记录左端点和长度,最后一次直接利用substr求得最短子串就欧克了。
class Solution {
public:
unordered_map<char, int> a, b;
unordered_set<char> us;
bool check(){
for(auto i : us){
if(a[i] < b[i]) return 0;
}
return 1;
}
string minWindow(string s, string t) {
int len = max(t.size(), s.size()) + 1;
int left = -1;
for(char ch : t) {
us.insert(ch);
b[ch]++;
}
bool flag = 1;
for(int l = 0, r = 0; l <= r && r < s.size();){
if(flag) a[s[r]]++;
if(check()) {
// cout << s.substr(l, r - l + 1) << endl;
if(r - l + 1 < len) {
//ans = s.substr(l, r - l + 1);
left = l;
len = r - l + 1;
}
a[s[l]]--;
l++;
flag = 0;
}
else{
r++;
flag = 1;
}
}
if(left >= 0) return s.substr(left, len);
return "";
}
};
用单调栈记录在i之前比heights[i]高的长度,并在出栈的过程中更新ans的值。保证单调栈的每一个元素都是记录左边比自己高的长度。
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
deque<pair<int, int>> q;
heights.emplace_back(-10000);
int n = heights.size(), ans = -1;
for(int i = 0; i < n; i++){
int len = 0;
while(!q.empty() && q.back().first >= heights[i]){
ans = max(ans, q.back().first * (q.back().second + len));
len += q.back().second;
q.pop_back();
}
q.push_back(make_pair(heights[i], len + 1));
}
return ans;
}
};
一遍过
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
set<ListNode*> s;
for(ListNode *i = headA; i != NULL; i = i->next){
s.insert(i);
}
int len = s.size();
for(ListNode *i = headB; i != NULL; i = i->next){
len = s.size();
s.insert(i);
if(len == s.size()) return i;
}
return NULL;
}
};
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
bool isPalindrome(ListNode* head) {
ListNode* i = head;
vector<int> v(1e6);
int h = 1, t;
while(i!=nullptr){
v[h++] = i->val;
i = i -> next;
}
t = h - 1;
h = 1;
while(h < t){
if(v[h++]!=v[t--]) return false;
}
return true;
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void f(TreeNode* root){
if(root == NULL){
return ;
}
f(root->left);
f(root->right);
TreeNode node = TreeNode(root->val, root->right, root->left);
root->left = node.left;
root->right = node.right;
}
TreeNode* invertTree(TreeNode* root) {
f(root);
return root;
}
};
大根堆
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int, vector<int>, less<int>> p;
for(auto i : nums) p.push(i);
for(int i = 1; i < k; i++) p.pop();
return p.top();
}
};
但我这个写法不是直接反转原本链表,而是重建了一个新的链表,原本链表没有删除。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode *i = head, *temp = nullptr, *root = nullptr;
while(i != NULL){
root = new ListNode(i->val, temp);
temp = root;
i = i->next;
}
return root;
}
};
直接反转原来的节点。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode *pre = nullptr, *curr = head;
while(curr){
ListNode *next = curr->next; //记录下一个节点的位置
curr->next = pre; //修改当前节点
pre = curr;
curr = next;
}
return pre;
}
};
经典BFS搜索
//这个代码不知道为啥粘上来就报错
经典dp
class Solution {
public:
int rob(vector<int>& nums) {
int len = nums.size(), ans = 0;
vector<int> dp(len, 0);
for(int i = 0; i < len; i++){
dp[i] = nums[i];
for(int j = 0; j < i - 1; j++){
dp[i] = max(dp[j] + nums[i], dp[i]);
}
ans = max(ans, dp[i]);
}
return ans;
}
};
写了一个很蠢的做法
class Solution {
public:
int majorityElement(vector<int>& nums) {
sort(nums.begin(), nums.end());
int len = nums.size(), temp = nums[0], sum = 0;
for(auto i : nums){
if(temp != i){
sum = 0;
temp = i;
}
sum++;
if(sum>len/2) return i;
}
return 0;
}
};
其实可以直接利用众数,直接返回
class Solution {
public:
int majorityElement(vector<int>& nums) {
sort(nums.begin(), nums.end());
return nums[nums.size() / 2];
}
};
学了一下Boyer-Moore 算法,O(N)的时间复杂度,O(1)的空间复杂度。
如果我们把众数记为+1,把其他数记为−1,将它们全部加起来,显然和大于 0,即如果一个数组有大于一半的数相同,那么任意删去两个不同的数字,新数组还是会有相同的性质。
class Solution {
public:
int majorityElement(vector<int>& nums) {
int a = nums[0], sum = 0;
for(int num : nums){
if(num == a) sum++;
else {
sum--;
if (sum < 0){
a = num;
sum = 1;
}
}
}
return a;
}
};
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
vector<int> a(nums.size()), b(nums.size()), ans(nums.size());
a[0] = nums[0], b[nums.size() - 1] = nums[nums.size() - 1];
for(int i = 1; i < nums.size(); i++){
a[i] = a[i-1] * nums[i];
b[nums.size() - 1 - i] = b[nums.size() - i] * nums[nums.size() - 1 - i];
}
ans[0] = b[1], ans[nums.size() - 1] = a[nums.size() - 2];
for(int i = 1; i < nums.size() - 1; i++){
ans[i] = a[i - 1] * b[i + 1];
}
return ans;
}
};
变成O(1)的空间复杂度的话,就把反方向的乘法直接一个一个乘进ans数组里。
随便写了一个dp就过了,但是没有官方题解写的好理解。
class Solution {
public:
bool wordBreak(string str, vector<string>& wordDict) {
int len = str.size();
vector<int> dp(len);
unordered_set<string> s;
for(auto ss : wordDict) s.insert(ss);
for(int i = 0; i < len; i++){
for(int j = 0; j <= i; j++){
string ss = str.substr(j, i - j + 1);
if(s.count(ss)){
if(j == 0) dp[i] = 1;
else if(dp[j - 1] > 0) dp[i] = max(dp[j - 1] + 1, dp[i]);
}
}
}
if(dp[len - 1] > 0) return 1;
else return 0;
}
};
这里dp其实不用计数,直接用bool就行。在dp数组前面多开一个dp[0],不用分类讨论,写起来会更美观 ↓
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
int len = s.size();
s = " " + s;
unordered_set<string> u;
for(auto ss : wordDict) u.insert(ss);
vector<bool> dp(len + 1);
dp[0] = true;
for(int i = 1; i <= len; i++){
for(int j = 1; j <= i; j++){
if(dp[j-1]&&u.count(s.substr(j, i - j + 1))) {
dp[i] = true;
break;
}
}
}
return dp[len];
}
};
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
unordered_set<int> s;
unordered_map<int,int> mp;
unordered_map<int, bool> b;
int ans = 0;
for(auto n : nums) s.insert(n), mp[n] = 1, b[n] = 0;
for(auto a : s) {
int i = a;
b[i] = 1;
while(s.count(i - 1)){
if(b[i - 1]) {
mp[a] += mp[i - 1];
break;
}
else{
b[i - 1] = 1, mp[a]++;
i--;
}
}
ans = max(ans, mp[a]);
}
return ans;
}
};
很基础的完全背包
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, amount + 1);
dp[0] = 0;
for(int i = 1; i <= amount; i++){
for(auto j : coins){
if(i - j < 0) continue;
else dp[i] = min(dp[i], dp[i-j] + 1);
}
}
if(dp[amount] == amount + 1) return -1;
else return dp[amount];
}
};
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<bool> v(nums.size() + 1);
vector<int> ans;
for(auto num : nums) v[num] = 1;
for(int i = 1; i <= nums.size(); i++){
if(!v[i]) ans.emplace_back(i);
}
return ans;
}
};
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
vector<int> a, b;
ListNode *head = new ListNode();
int sum1 = 0, sum2 = 0;
while(l1 != nullptr){
a.emplace_back(l1 -> val);
sum1++;
l1 = l1 -> next;
}
while(l2 != nullptr){
b.emplace_back(l2 -> val);
sum2++;
l2 = l2 -> next;
}
a.emplace_back(0), b.emplace_back(0);
ListNode *node = head;
int flag = 0, i = 0, j = 0;
for(; i < sum1 && j < sum2; i++, j++){
ListNode *n = new ListNode((a[i] + b[j] + flag) % 10);
node -> next = n;
node = n;
if(a[i] + b[j] + flag >= 10) flag = 1;
else flag = 0;
}
for(; i < sum1; i++) {
ListNode *n = new ListNode((a[i] + flag) % 10);
node -> next = n;
node = n;
if(a[i] + flag >= 10) flag = 1;
else flag = 0;
}
for(; j < sum2; j++) {
ListNode *n = new ListNode((b[j] + flag) % 10);
node -> next = n;
node = n;
if(b[j] + flag >= 10) flag = 1;
else flag = 0;
}
if(flag){
ListNode *n = new ListNode(1);
node -> next = n;
}
return head -> next;
}
};
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for(auto num : nums) sum += num;
if(sum % 2 == 1) return 0;
vector<bool> dp(sum / 2 + 1);
dp[0] = 1;
for(auto num : nums){
for(int i = sum / 2; i >= 0; i--){
if(i - num < 0) break;
if(dp[i - num] == 1) dp[i] = 1;
}
if(dp[sum / 2]) return 1;
}
return 0;
}
};
class Solution {
public:
int maxProfit(vector<int>& prices) {
int mi = 10000, ans = 0;
for(int i = 0; i < prices.size(); i++){
if(mi > prices[i]) mi = prices[i];
else ans = max(ans, prices[i] - mi);
}
return ans;
}
};
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> mp;
unordered_set<int> s;
priority_queue<pair<int, int>> q;
vector<int> ans;
for(auto num : nums){
mp[num]++;
s.insert(num);
}
for(auto num : s){
q.push({mp[num], num});
}
for(int i = 1; i <= k; i++){
ans.emplace_back(q.top().second);
q.pop();
}
return ans;
}
};
class Solution {
public:
int B(int n){
int res = 0;
while(n){
n &= (n - 1);
res++;
}
return res;
}
vector<int> countBits(int n) {
vector<int> ans;
for(int i = 0; i <= n; i++) ans.emplace_back(B(i));
return ans;
}
};
class Solution {
public:
void moveZeroes(vector<int>& nums) {
for(int r = 0, l = 0; l < nums.size(); l++){
r = max(r, l);
if(nums[l] == 0){
while(r < nums.size() && nums[r] == 0) r++;
if(r < nums.size()) swap(nums[l], nums[r]);
}
}
}
};
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int ans = 0;
vector<int> dp(nums.size(), 1);
for(int i = 0; i < nums.size(); i++){
for(int j = 0; j < i; j++){
if(nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
}
ans = max(ans, dp[i]);
}
return ans;
}
};
class Solution {
public:
int findDuplicate(vector<int>& nums) {
sort(nums.begin(), nums.end());
for(int i = 1; i < nums.size(); i++){
if(nums[i] == nums[i - 1]) return nums[i];
}
return 0;
}
};
class Solution {
public:
int numSquares(int n) {
vector<int> nums, dp(n + 1, n);
dp[0] = 0;
for(int i = 1; i * i <= n; i++) nums.emplace_back(i * i);
for(int i = 0; i <= n; i++){
for(auto j : nums){
if(i - j < 0) continue;
dp[i] = min(dp[i], dp[i - j] + 1);
}
}
return dp[n];
}
};
观察到右下角的一直大于其左上的所有元素。但是看到数据范围,懒得找规律了,直接一个很简单的遍历就过了
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int h = matrix.size(), w = matrix[0].size();
for(int i = 0; i < h; i++){
for(int j = 0; j < w; j++){
if(matrix[i][j]==target) return 1;
}
}
return 0;
}
};
但其实是观察图形题,看了一下题解,“z”字型搜索:
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int h = matrix.size(), w = matrix[0].size();
int x = 0, y = w - 1;
while(x < h && y >= 0){
if(matrix[x][y] == target) return true;
else if(matrix[x][y] > target) y--;
else x++;
}
return false;
}
};
class Solution {
public:
vector<string> ans;
int num;
void dfs(string s, int len1, int len2){
if(len1 + len2 == num * 2){
if(len1 == num){
int flag = 0;
bool st = 1;
for(char ch : s){
if(ch == '(') flag++;
else flag--;
if(flag < 0){
st = 0;
break;
}
}
if(st) ans.emplace_back(s);
}
return;
}
dfs(s + '(', len1 + 1, len2);
dfs(s + ')', len1, len2 + 1);
}
vector<string> generateParenthesis(int n) {
num = n;
string s;
dfs(s, 0, 0);
return ans;
}
};
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
vector<string> s = strs;
unordered_map<string, vector<string>> mp;
vector<vector<string>> ans;
unordered_set<string> a;
for(int i = 0; i < strs.size(); i++){
sort(s[i].begin(), s[i].end());
a.insert(s[i]);
mp[s[i]].emplace_back(strs[i]);
}
for(auto ss : a) ans.emplace_back(mp[ss]);
return ans;
}
};
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> ans;
sort(nums.begin(), nums.end());
do{
ans.emplace_back(nums);
}while(next_permutation(nums.begin(), nums.end()));
return ans;
}
};
class Solution {
public:
int n;
vector<int> v;
set<vector<int>> st;
void dfs(vector<int> a, int curr){
if(curr == n) {
sort(a.begin(), a.end());
st.insert(a);
}
else{
for(auto i : v){
if(curr + i > n) break;
a.emplace_back(i);
dfs(a, curr + i);
a.pop_back();
}
}
return;
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
sort(candidates.begin(), candidates.end());
n = target, v = candidates;
vector<int> a;
vector<vector<int>> ans;
dfs(a, 0);
for(auto s : st) ans.emplace_back(s);
return ans;
}
};
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n + 1);
dp[0] = 1, dp[1] = 1;
for(int i = 2; i <= n; i++){
dp[i] += dp[i - 1];
dp[i] += dp[i - 2];
}
return dp[n];
}
};
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0;
vector<vector<int>> dp(prices.size(), vector<int>(2));
for(int i = 0; i < prices.size(); i++){
dp[i][0] -= prices[i];
for(int j = 0; j < i - 1; j++){
dp[i][0] = max(dp[j][1] - prices[i], dp[i][0]);
}
for(int j = 0; j < i; j++){
dp[i][1] = max(dp[j][0] + prices[i], dp[i][1]);
}
ans = max(ans, dp[i][1]);
}
return ans;
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int ans = 0;
unordered_map<TreeNode*, pair<int,int>> mp;
void dfs(TreeNode *node){
int l, r;
if(node -> left == nullptr) {
mp[node].first = 0;
l = 0;
}
else{
dfs(node -> left);
l = max(mp[node -> left].first, mp[node -> left].second) + 1;
}
if(node -> right == nullptr) {
mp[node].second = 0;
r = 0;
}
else{
dfs(node -> right);
r = max(mp[node -> right].first, mp[node -> right].second) + 1;
}
mp[node] = {l, r};
ans = max(ans, l + r);
}
int diameterOfBinaryTree(TreeNode* root) {
dfs(root);
return ans;
}
};
class Solution {
public:
bool check(vector<int>& nums){
bool flag = 1;
for(int i = nums.size() - 1; i > 0; i--){
if(nums[i] > nums[i - 1]){
flag = 0;
break;
}
}
return flag;
}
void nextPermutation(vector<int>& nums) {
if(check(nums)) {
sort(nums.begin(), nums.end());
return;
}
int a = nums.size() - 1;
for(int i = nums.size() - 1; i > 0; i--){
if(nums[i] > nums[i - 1]){
a = i;
break;
}
}
for(int i = nums.size() - 1; i >= a; i--){
if(nums[a - 1] < nums[i]){
swap(nums[a - 1], nums[i]);
break;
}
}
sort(nums.begin() + a, nums.end());
}
};
直接用暴力写的,没有用到二叉线索树的性质,直接把节点存起来,然后根据val排序后利用前缀和修改指针的值。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<pair<int, TreeNode*>> v;
void dfs(TreeNode* node){
if(node == nullptr) return;
v.emplace_back(node -> val, node);
dfs(node -> left), dfs(node -> right);
}
TreeNode* convertBST(TreeNode* root) {
dfs(root);
sort(v.begin(), v.end(), greater<pair<int, TreeNode*>>());
if(v.size() <= 1) return root;
vector<int> sum(v.size());
sum[0] = v[0].first;
for(int i = 1; i < v.size(); i++) {
sum[i] = sum[i - 1] + v[i].first;
v[i].second -> val = sum[i];
}
return root;
}
};
其实利用性质更简单,先累加右边在累加左边:
class Solution {
public:
int sum = 0;
TreeNode* convertBST(TreeNode* root) {
if(root != nullptr){
convertBST(root -> right);
sum += root -> val;
root -> val = sum;
convertBST(root->left);
}
return root;
}
};
想不到非暴力双指针(n^2)的做法。
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int n = nums.size(), ans = 0;
vector<int> sum(n + 1);
for(int i = 1; i <= n; i++){
sum[i] = sum[i - 1] + nums[i - 1];
}
for(int i = 1; i <= n; i++){
for(int j = 1; i >= j; j++){
if(sum[i] - sum[j - 1] == k) ans++;
}
}
return ans;
}
};
学了一下题解的前缀和+哈希。
根据之前的前缀和的解法核心是判断sum[i] - sum[j - 1] == k,因此也可以推成sum[j - 1] == sum[i] - k。直接从左到右遍历一边,每次记录sum[j - 1]的个数就行了。
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int, int> mp;
mp[0] = 1;
int sum = 0, ans = 0;
for(int num : nums){
sum += num;
int a = sum - k;
if(mp.count(a)) ans += mp[a];
mp[sum]++;
}
return ans;
}
};
class Solution {
public:
bool isValid(string s) {
stack<char> st;
for(char &ch : s){
if(ch == '(' || ch == '[' || ch == '{')
st.push(ch);
else{
if(st.empty()) return false;
else {
if(ch == ')' && st.top() != '(') return false;
if(ch == '}' && st.top() != '{') return false;
if(ch == ']' && st.top() != '[') return false;
st.pop();
}
}
}
return st.empty() ? 1 : 0;
}
};
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
int len = 0;
ListNode *node = head, *pre = nullptr;
while(node -> next != nullptr){
node = node -> next;
len++;
}
n = len - n + 1;
node = head;
for(int i = 1; i <= n; i++){
pre = node;
node = node -> next;
}
if(pre == nullptr) return head -> next;
pre -> next = node -> next;
return head;
}
};
class Solution {
public:
unordered_map<char, string> mp{
{'2', "abc"},
{'3', "def"},
{'4', "ghi"},
{'5', "jkl"},
{'6', "mno"},
{'7', "pqrs"},
{'8', "tuv"},
{'9', "wxyz"}
};
vector<string> ans;
void dfs(string cur, int index, string digits){
if(index == digits.size()){
ans.emplace_back(cur);
return;
}
char ch = digits[index];
for(auto c : mp[ch]){
dfs(cur + c, index + 1, digits);
}
}
vector<string> letterCombinations(string digits) {
if(digits != "")
dfs("", 0, digits);
return ans;
}
};
class Solution {
public:
bool check(deque<char> &q){
set<char> s;
for(auto i : q){
s.insert(i);
}
if(s.size() == q.size()) return 1;
else return 0;
}
int lengthOfLongestSubstring(string s) {
deque<char> q;
int ans = 0;
for(int i = 0; i < s.size(); i++){
q.push_back(s[i]);
if(check(q)) ans = max(ans, (int)q.size());
else{
while(q.front() != s[i])
q.pop_front();
q.pop_front();
}
}
return ans;
}
};
其实想复杂了,就是一个贪心问题,不用考虑往回走。每次记录能到达最右端的下标就行,只要最后一个下标<=max,就是可以到达。
class Solution {
public:
bool canJump(vector<int>& nums) {
queue<int> q;
vector<bool> vis(nums.size());
q.push(0);
vis[0] = 1;
while(!q.empty()){
int a = q.front();
q.pop();
for(int i = 1; i <= nums[a] && a - i >= 0; i++)
if(!vis[a - i]) q.push(a - i), vis[a - i] = 1;
for(int i = 1; i <= nums[a] && a + i < nums.size(); i++)
if(!vis[a + i]) q.push(a + i), vis[a + i] = 1;
if(vis[nums.size() - 1]) return 1;
}
return 0;
}
};
class Solution {
public:
int uniquePaths(int m, int n) {
int dp[m][n];
for(int i = 0; i < m; i++) dp[i][0] = 1;
for(int i = 0; i < n; i++) dp[0][i] = 1;
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
和上面这题一样。
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int dp[m][n];
dp[0][0] = grid[0][0];
for(int i = 1; i < m; i++) dp[i][0] = dp[i - 1][0] + grid[i][0];
for(int i = 1; i < n; i++) dp[0][i] = dp[0][i - 1] + grid[0][i];
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[m - 1][n - 1];
}
};
class Solution {
public:
int findUnsortedSubarray(vector<int>& nums) {
vector<int> v = nums;
sort(v.begin(), v.end());
int r = -100, l = 0;
for(int i = 0; i < nums.size(); i++){
if(v[i] != nums[i]) {
l = i;
break;
}
}
for(int i = v.size() - 1; i >= 0; i--){
if(v[i] != nums[i]) {
r = i;
break;
}
}
return max(0, r - l + 1);
}
};
常规二维dp直接算。
class Solution {
public:
int minDistance(string word1, string word2) {
int m = word1.size(), n = word2.size();
word1 = " " + word1, word2 = " " + word2;
int dp[m + 1][n + 1];
for(int i = 0; i <= n; i++) dp[0][i] = i;
for(int i = 0; i <= m; i++) dp[i][0] = i;
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(word1[i] == word2[j])
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]) + 1, dp[i - 1][j - 1]);
else dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
}
return dp[m][n];
}
};
class Solution {
public:
void sortColors(vector<int>& nums) {
int l = 0;
while(l < nums.size() && nums[l] == 0) l++;
for(int i = l + 1; i < nums.size(); i++){
if(nums[i] == 0){
swap(nums[i], nums[l]);
l++;
}
while(l < nums.size() && nums[l] == 0) l++;
}
while(l < nums.size() && nums[l] == 1) l++;
for(int i = l + 1; i < nums.size(); i++){
if(nums[i] == 1){
swap(nums[i], nums[l]);
l++;
}
while(l < nums.size() && nums[l] == 0) l++;
}
}
};
前序遍历直接存一下就好了,比较基础
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<TreeNode*> v;
void dfs(TreeNode* root){
if(root == nullptr) return;
v.emplace_back(root);
dfs(root -> left);
dfs(root -> right);
}
void flatten(TreeNode* root) {
dfs(root);
for(int i = 1; i < v.size(); i++){
root -> left = nullptr;
root -> right = v[i];
root = root -> right;
}
}
};
就是这个ans.emplace_back(root -> val)的位置,这个就是计入根的位置,前面就是前序遍历,中间就是中序遍历,后面就是后续遍历。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> ans;
void dfs(TreeNode* root){
if(root == nullptr) return;
dfs(root -> left);
ans.emplace_back(root -> val);
dfs(root -> right);
}
vector<int> inorderTraversal(TreeNode* root) {
dfs(root);
return ans;
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int ans = 0;
void dfs(TreeNode* root, int num){
if(root == nullptr) {
ans = max(ans, num - 1);
return;
}
dfs(root -> right, num + 1);
dfs(root -> left, num + 1);
}
int maxDepth(TreeNode* root) {
dfs(root, 1);
return ans;
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
queue<pair<TreeNode*, int>> q;
int flag = 1;
q.push({root, 1});
vector<int> v;
while(!q.empty()){
TreeNode* a = q.front().first;
int b = q.front().second;
q.pop();
if(a == nullptr) continue;
if(flag != b) {
flag = b;
ans.emplace_back(v);
v = vector<int>();
}
v.emplace_back(a -> val);
q.push(make_pair(a -> left, b + 1));
q.push(make_pair(a -> right, b + 1));
}
if(!v.empty()) ans.emplace_back(v);
return ans;
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void dfs1(vector<int> &v, TreeNode* root){
if(root == nullptr) {
v.emplace_back(-1000);
return;
}
v.emplace_back(root -> val);
dfs1(v, root -> left);
dfs1(v, root -> right);
}
void dfs2(vector<int> &v, TreeNode* root){
if(root == nullptr) {
v.emplace_back(-1000);
return;
}
v.emplace_back(root -> val);
dfs2(v, root -> right);
dfs2(v, root -> left);
}
bool isSymmetric(TreeNode* root) {
if(root == nullptr) return 1;
vector<int> a, b;
dfs1(a, root -> left), dfs2(b, root -> right);
return a == b;
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> v;
void dfs(TreeNode* root){
if(root == nullptr) return;
dfs(root -> left);
v.emplace_back(root -> val);
dfs(root -> right);
}
bool isValidBST(TreeNode* root) {
dfs(root);
for(int i = 1; i < v.size(); i++){
if(v[i] <= v[i - 1]) return 0;
}
return 1;
}
};
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size(), ans = nums[0];
vector<vector<int>> dp(n, vector<int>(2));
dp[0][0] = nums[0], dp[0][1] = nums[0];
for(int i = 1; i < n; i++){
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]) + nums[i];
dp[i][1] = nums[i];
ans = max(ans, max(dp[i][0], dp[i][1]));
}
return ans;
}
};
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
set<int> start;
unordered_map<int, int> end;
vector<vector<int>> ans;
int n = intervals.size();
for(int i = 0; i < n; i++){
start.insert(intervals[i][0]);
end[intervals[i][0]] = max(end[intervals[i][0]], intervals[i][1]);
}
int s = 0, e = -1;
for(auto i : start){
if(i > e){
if(s <= e) {
vector<int> temp{s, e};
ans.emplace_back(temp);
}
s = i, e = end[i];
}
else e = max(end[i], e);
}
vector<int> temp{s, e};
ans.emplace_back(temp);
return ans;
}
};
class Solution {
public:
void rotate(vector<int>& nums, int k) {
vector<int> ans;
int n = nums.size();
k = k % n;
for(int i = n - k; i < n; i++)
ans.emplace_back(nums[i]);
for(int i = 0; i < n - k; i++)
ans.emplace_back(nums[i]);
nums = ans;
}
};
不是这个为啥会被标称困难。。。
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size(), m = nums2.size();
vector<int> v;
int i = 0, j = 0;
for(; i < n && j < m;){
if(nums1[i] < nums2[j]) v.emplace_back(nums1[i++]);
else v.emplace_back(nums2[j++]);
}
for(; i < n; i++) v.emplace_back(nums1[i]);
for(; j < m; j++) v.emplace_back(nums2[j]);
int l = 0, r = n + m - 1;
for(; l <= r; l++, r--){
}
double a = v[l - 1], b = v[r + 1];
return (a + b) / 2;
}
};
更新节点
2025-01-24
2025-01-25
2025-01-26
2025-01-28
2025-01-30
2025-01-31
2025-02-01
2025-02-02
2025-02-03 【小记:终于刷完1/3的题目了,论文也一审返修了,很开心。坚持加油!】
2025-02-07 【小记:陪外婆住院还被导师抓去写本子了,进度突然变慢了SOS】
2025-02-09
2025-02-10
2025-02-12 【小记:刷完一半题目了!】
2025-02-15
2025-02-21 【小记:这段时间弄论文re弄的我好苦啊,幸好都暂告一段落了,现在准备开始提升自我了】
2025-02-22 【小记:70/100 !!!还有30题就刷完了】
2025-02-23
2025-02-24
2025-03-02 【小记:前几天处理论文录用相关的问题去了,也是因为太happy庆祝去了,各种进度断更一周,今天恢复持续更新】
2025-03-03 【小记:剩的中等题不多了,马上要攻坚克服困难了】
2025-03-10
2025-03-11 【小记:剩下的好难啊 现在是(86 / 100),就先到这里为止吧】
整个的刷题记录进展:


