CO-Representation and Computation of Data
Published:
今天是第二章——数据的表示和运算。本章探讨数据如何在计算机中表示,运算器如何实现数据的算数、逻辑运算
零、回顾
计算机硬件组成框架如下:

主机 = CPU + M.M, CPU = 运算器 + 控制器
他们的详细组成和内容如下:

本章开始介绍运算器的相关原理
一、数制与编码
1.1 进位计数制

十进制转换为二进制需要分为两个部分:整数部分和小数部分
整数部分使用的是除基取余的方法
小数部分使用的是乘基取整的方法
这里值得注意的是:任意二进制小数都可以用十进制小数表示,但是并不是任意十进制小数都可以用二进制小数表示
二进制转换为十进制,如图所示,可以直接加上所有1对应位置上的权值;



1.2 BCD码
BCD 码就是用 4 个 bit 位(二进制数)对应 1 个十进制位,是一种二进制的数字编码形式,用二进制编码来代替十进制代码。

- BCD码的运算

- 余 3 码(无权码)

- 2421 码

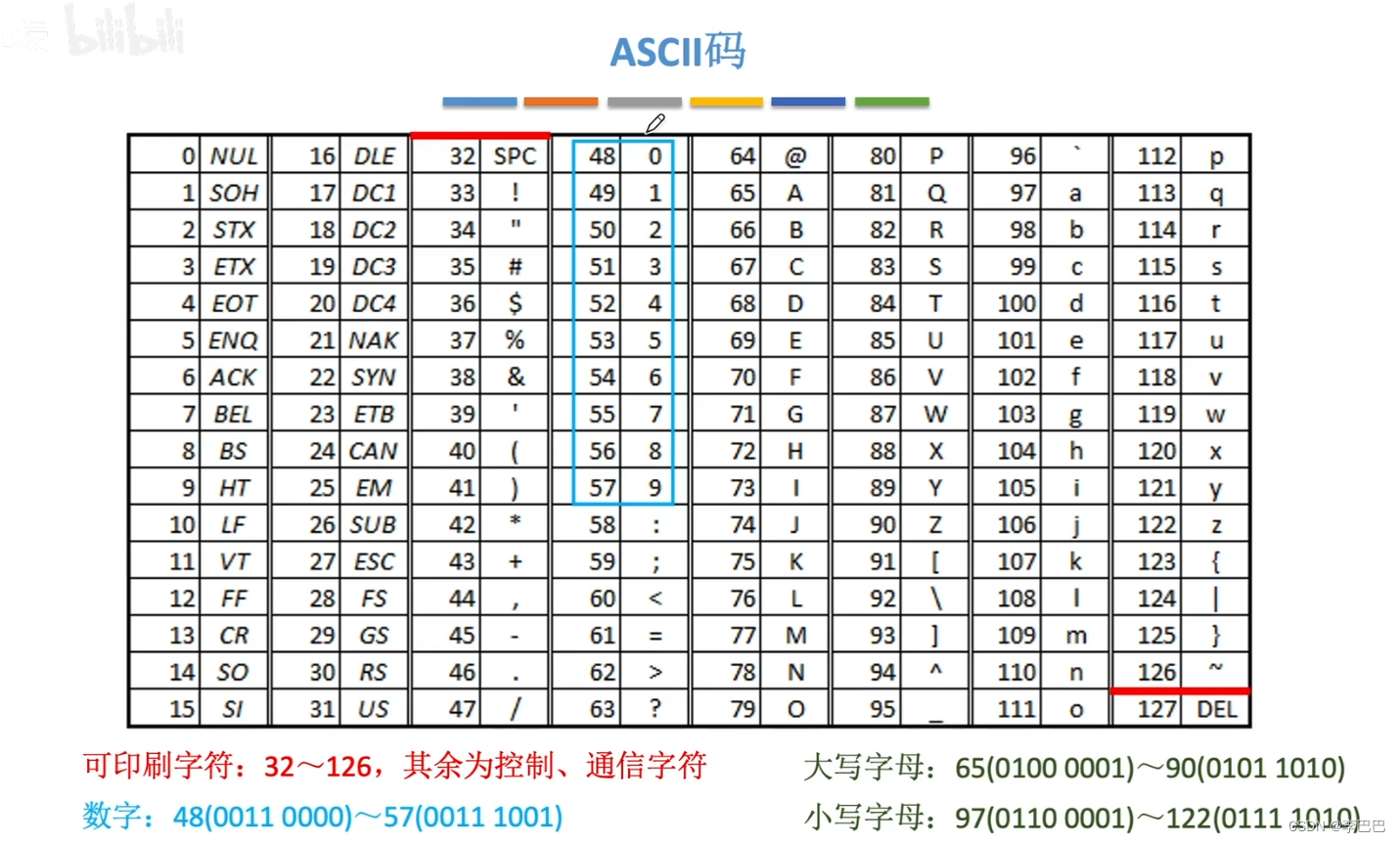
1.3 ASCII 码
我们知道我们日常见到的数字(0~9)、符号比如:#、%、+、@等、英语字母如:(A~z)、(a~z),它们在计算机中都是以二进制来表示存储的,咱们可以用不同的二进制数来表示,但是为了统一化、使大家的相互通信可以正常进行,那么就必须制定一套统一的标准来规范它,由此ASCII码随之诞生,大家都遵从这一统一的标准进行数据的通信和交流。
1.4 校验码
校验码中我们最常见的有以下三种:奇偶校验码、海明校验码和CRC循环冗余码;
- 奇偶校验码:这也是最常见的一种校验码,他又分为奇校验码和偶校验码;奇校验码指的是整个校验码(包含信息位和校验位)中1的个数是奇数个,而偶校验码指的是整个校验码中1的个数为偶数个;

非常简单明了,但是我们需要知道奇偶校验码是具有局限性的,只能发现奇数位的错误,不能发现偶数位的错误而且不能纠正错误。那为什么还会说它是最常见的呢?因为我们在通信最常发生的便是一位数据的错误了。奇偶校验码的码距 d = 2 ,仅能检测出奇数位错误,无纠错能力。
- 海明校验码:海明码的特点有四个字:纠一检二(纠正一位错误,检测两位错误)海明码往往会在首部加上全检验进行偶校验码;

- CRC循环冗余码:循环冗余码应用的场景主要是有大量数据传输时,通过与生成多项式做模2运算得到一个新的二进制码;当接收端接收到数据时,再用相同的多项式进行模2运算,如果结果为0则表示数据没有错误;接收端检测时检测出一位数据错误后,纠正的方法包括:请求重发、删除数据以及通过余数值进行纠正。

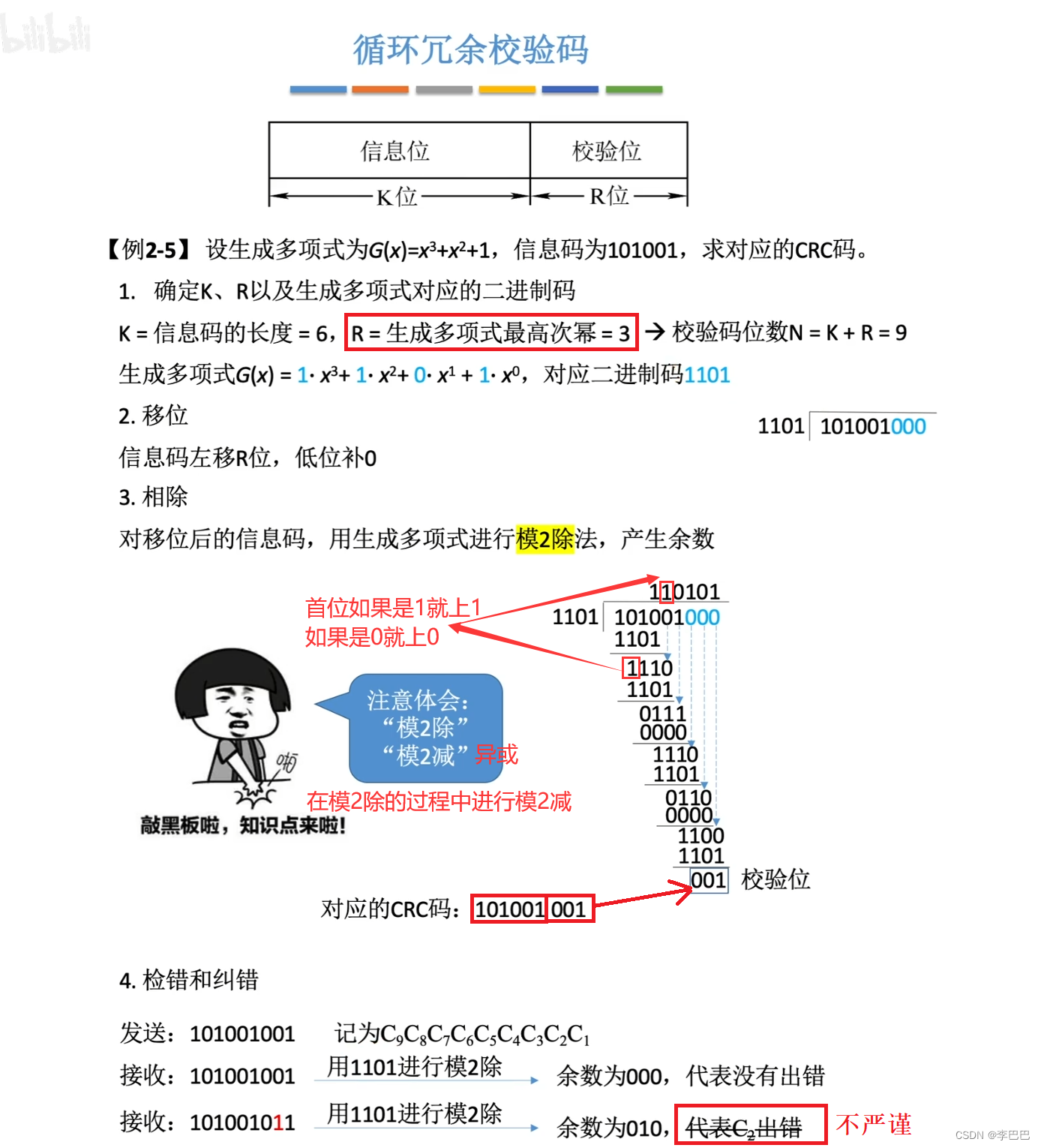
理论上,循环冗余校验码的检错能力有以下特点:可检测出所有奇数个错误,可检测出所有双比特的错误,可检测所有小于等于检验位长度的连续错误。CRC 循环冗余码实际应用中一般只用来“检错”,不用来“纠错”
二、定点数的表示和运算
2.1 定点数的表示
(1)无符号
整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值。若机器字长为 8 位,则数的表示范围 0~255。(通常只有无符号整数,没有无符号小数)
(2)有符号(原码、反码、补码、移码)
在机器中,数的正负我们无法识别,但是我们可以用二进制数来代替正负号。一般‘0’为正,‘1’为负,符号位一般在有效数的最前面。

在计算机中表示一个定点数包括原码、补码、反码和移码;
原码:针对正数的原码,我们会在最高位添加0,针对负数,我们会在最高位添1,其他位按照无符号数处理即可;原码是有正零和负零之分的,因此定点整数原码的表示范围只是:-(2n-1)~2n-1(关于原点对称),定点小数也是一样;
补码:补码可以说是这些码中最重要的,因为在计算机中存储的定点数便是补码形式,首先我们要知道为什么需要补码,因为在计算机的内部进行加减运算时,我们会发现两个正数相加还好,通过加法器就能实现,但是当两个正数相减时,这个减法器可就不好设计了,因此出现了补码。
由于计算机硬件的位数是固定的,也就是寄存器中的位数是固定的,那么当两个数相加超过寄存器位数所能表示的最大整数时,其实就相当于进行了一次简单的模运算。打一个简单的比方:假设现在有三位寄存器,最大表示7(即111),我现在有两个数5(即101)和3(即011),两个数相加得到1000,但是因为寄存器只有三位,那么剩下的便只有000了,那如果变成了减法,其实5-3不就是5+(-3),结果2也可以表示成10,那么-3便也可以用5来替代;根据这一规律,我们发现负数是可以用与寄存器能够表示的最大数范围取模的正数表示的;
具体实现其实很简单,正数的补码和原码相同,负数的补码就是原码除了符号位取反加一。补码的范围需要注意的是,补码的-0即1000……(n+1位)用来表示的是-2n,范围是:-2n到2n-1;小数将-0用来表示了-1,范围是:-1到1-2-n;
反码:反码是补码产生的一个衍生物,我们知道补码是原码取反加1,是的,你可能已经猜到了,原码不加1只取反便是反码了,当然这只是针对负数,正数就是用原码表示;范围同原码。
移码:移码是把补码的符号位取反;看似十分简单,但是移码非常有用的,因为移码保持了原有数据的大小顺序,所以,移码越大真值越大,当有找最大最小值或者大小比较问题时,我们首先需要想到移码;移码因为来自补码,所以范围同补码;

一些之前学习的Tips:
在补码表示法中,真值“0”的补码是唯一的,即0.00···0,而补码1.00···0则代表“1”(二进制小数为例)
由于源码“0”的表示有“+0”和“-0”之分,因此范围是$[-(2^n-1), 2^n-1]$
补码由于没有这个概念,源码“-0”对应的二进制表示在补码中表示绝对值最大的负数,因此范围是$[-2^n, 2^n-1]$
2.2 定点数的运算
(1)移位运算
移位:通过改变各个数码位和小数点的相对位置,从而改变各数码位的位权。可用移位运算实现乘法、除法。
算术位移
原码的算术移位:符号位保持不变,仅对数值位进行移位。
右移:高位补0,低位舍弃。若舍弃的位 = 0,则相当于 ÷ 2 ;若舍弃的位 ≠ 0,则会丢失精度
左移:低位补0,高位舍弃。若舍弃的位 = 0,则相当于 × 2 ;若舍弃的位 ≠ 0,则会出现严重错误
反码的算术位移

- 补码的算术位移

逻辑位移
- 逻辑右移:高位补 0,低位舍弃
- 逻辑左移:低位补 0,高位舍弃
逻辑位移可以看作对 “无符号数” 的算术移位。
循环位移

(2)加减运算
原码的加减运算

补码的加减运算:对于补码来说,无论加法还是减法,最后都会转变成加法,由加法器实现运算,符号位也参与运算。

溢出判断

(3)补码一位乘

